4.6. Operators¶

Now that we know how to store data in variables, let’s learn how to create new values from existing data. Run the following code. It stores values in two variables, number_of_days and hours_per_day, then prints the result of several expressions.

Try changing one or more of the operators in lines 4 - 9 (+, -, *, /, **) to display a different output.

An operator tells Python to perform an action on two values. Operators may be a single character (like +), double characters (like **), or keywords.

The values an operator works on are called operands. Operands may be simple numbers or strings, or they be variables.

Operands are the values on either side of the operator.

When Python finds an operator, it evaluates the expression and returns a new value. When a variable is used in an expression (like number_of_days - 5), the variable’s stored value is evaluated in the expression.

4.6.1. Math Operators¶

Some of the most common operators perform simple math calculations. These operators behave just like their similar symbols in the world of math. Many of the symbols are probably familiar to you. However, there are two operators that are commonly used in programming but not much in math class.

Basic Math Operators¶
Operator	Description	Example
`+`	Adds two values (operands)	`2 + 3` returns `5`
`-`	Subtracts the first operand by the second	`2 - 3` returns `-1`
`*`	Multiplies two operands	`2 * 3` returns `6`
`/`	Divides the first operand by the second	`3 / 2` returns `1.5`
`**`	Takes the first operand and raises it to the power of the second. (first value)^{second value}	`3 2` returns `9` `5 3` returns `125`
`//`	Divides the first operand by the second and rounds down to a whole number. This is called floor division and is discussed immediately below.	`3 // 2` returns `1`
`%`	This is called the modulus operator. It returns the remainder after dividing the first operand by the second. It is discussed below.	`5 % 2` returns `1` `10 % 2` returns `0`

4.6.1.1. The `//` Operator¶

Whenever Python performs division with /, the value returned is a float data type.

Example

print(3 / 2)
print(10 / 10)
print(4 / 3)

Console Output

5
0
3333333333333333

As we see above, even for results that are whole numbers, like 10/10, the data type returned is a float, it contains a decimal.

If we want the result of a division to be an integer, we can convert it using the int() function as we saw in the type conversion section. In line 2 above, the syntax would be print(int(10 / 10)), giving an output of 1 instead of 1.0.

This situation, called floor division, is common enough that Python gives us a shortcut with the // operator. It divides two values and rounds the result DOWN to the next smallest integer, regardless of any decimal values.

Example

print(4 / 3, 4 // 3)
print(99 / 10, 99 // 10)

print(-3 / 2, -3 // 2)
print(-99 / 10, -99 // 10)

Console Output

1.3333333333333333    1
9.9    9
-1.5   -2
-9.9   -10

Note

We need to be careful when we consider negative numbers. Rounding down means making a larger negative value. While 9.9 rounds down to 9, -9.9 rounds down to -10.

Also, remember that the int() function removes the decimals without rounding. int(-99 / 10) returns -9, but -99 // 10 returns -10.

4.6.1.2. The `%` Operator¶

The modulus operator (%) takes two integers, divides them, and returns the remainder. Consider these examples, which might bring up fond memories of doing long division:

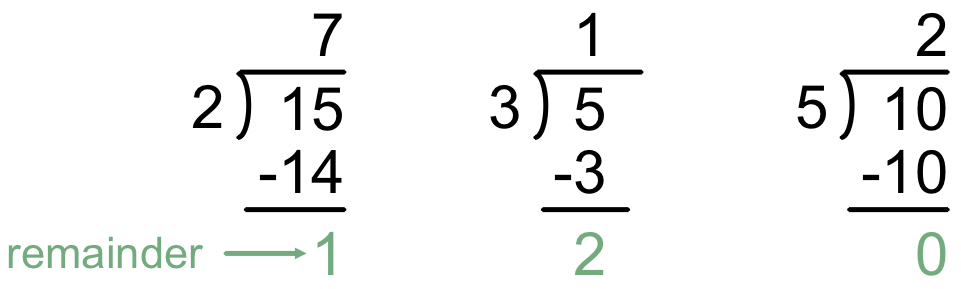
The modulus returns the remainder of a division.

In the first calculation, 2 does not go into 15 evenly. 2 * 7 = 14, which is too small, but 2 * 8 = 16, which is too large. 2 goes into 15 seven times, but this leaves a remainder of 1. Similarly, 3 goes into 5 one time, leaving a remainder of 2. Finally, 5 goes into 10 exactly 2 times, with no remainder left over.

The modulus operator divides the first operand by the second and returns the value of the remainder. So 15 % 2 returns 1, 5 % 3 returns 2, and 10 % 5 returns 0.

Example

Run the following code to see how % works.

Try changing the numbers on either side of the % operator and check the results.

You may be currently wondering:

Why would I EVER want to use a modulus?

Well, you will. However, we probably won’t convince you right now, at least with words.

Experience is the best teacher. As you continue with this course, you will find yourself using % more than you expect.

Tip

An integer, num, is even when num % 2 is 0, and it is odd when num % 2 is 1.

The value returned by a % b will be from 0 to b (not including b).

Fun Fact

The operation that the modulus symbol performs is called modulo.

4.6. Operators¶

4.6.1. Math Operators¶

4.6.1.1. The // Operator¶

4.6.1.2. The % Operator¶

4.6.2. Check Your Understanding¶

4.6.1.1. The `//` Operator¶

4.6.1.2. The `%` Operator¶