Congratulations! Identifying the base case is often the trickiest part of building a recursive function.
We've made it this far with combineEntries:
1function combineEntries(arrayName){
2 if (arrayName.length <= 1){
3 return arrayName[0];
4 } else {
5 //call combineEntries again
6 }
7}
Now we are ready to take the next step.
To help visualize what happens during recursion, let's start with the base case
['L']:
Nothing complicated here. combineEntries sees only one item in the array,
so it returns 'L'.
Now consider an array with two elements, ['L', 'C']:

In this case, combineEntries executes the else statement. We have no
code for this yet, but we can still consider the logic:
combineEntries returns 'L' and calls itself again using what is left
inside the array (['C']).['C'], which is the base case, combineEntries returns
'C'.'L' and 'C' get combined and returned as the final
result.Next, consider an array with three elements ['L', 'C', '1']:
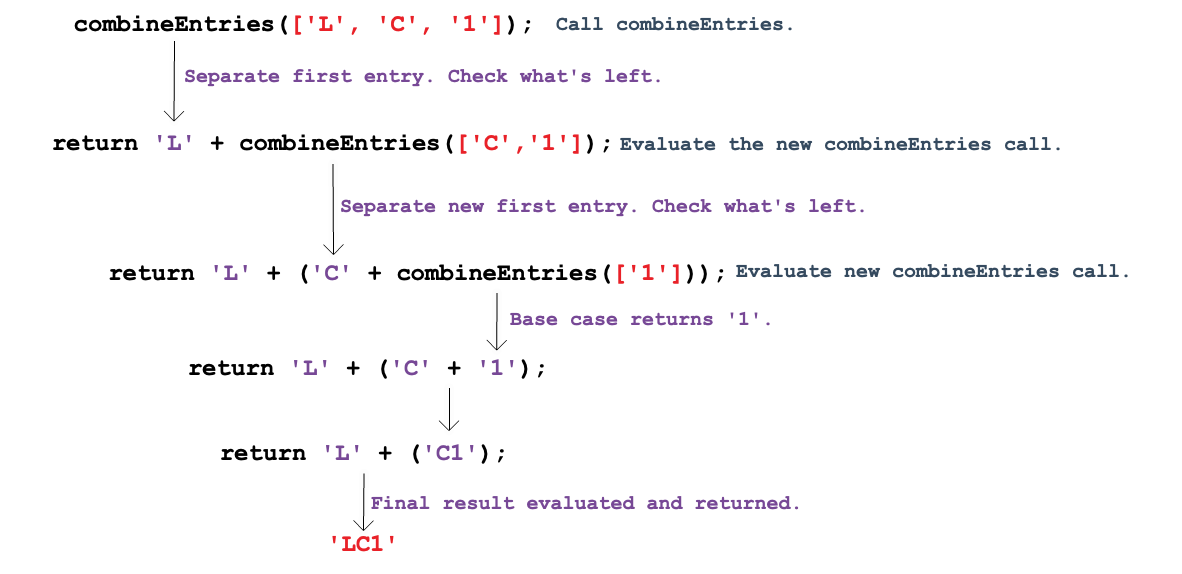
As before, combineEntries executes the else statement, and we can
follow the logic:
combineEntries returns 'L' and calls itself again using what is left
inside the array (['C', '1']).['C', '1'], combineEntries returns 'C' and calls
itself again using what is left inside the array (['1']).['1'], which is the base case, combineEntries returns
'1'.'C' and '1' get combined and returned.'L' and 'C1' get combined and returned as the final
result.As we make the array longer, combineEntries calls itself more times. Each
call evaluates a smaller and smaller section of the array until reaching the
base case. This sets up a series of return events - each one selecting a
single entry from the array. Rather than building 'LC101' from left to
right, recursion constructs the string starting with the base case and
adding new characters to the front:
| Value Returned | Description |
|---|---|
'1' |
Base case. Returns the element from an array of length 1. |
'01' |
Combines the first element from an array of length 2 with the base case value. |
'101' |
Combines the first element from an array of length 3 with the two previous values. |
'C101' |
Combines the first element from an array of length 4 with the three previous values. |
'LC101' |
Combines the first element from an array of length 5 with the four previous values. |
Recursive processes all follow this approach. Each call to the function reduces a problem into a slighly smaller piece. The reduction continues until reaching the simplest possible form---the base case. The base case is then solved, and this creates a starting point for completing all of the previous steps.
So how do we code the else statement in combineEntries? Recall what
needs to happen each time the statement runs:
combineEntries again with a smaller array.Bracket notation takes care of part a: arrayName[0].
For part b, remember that the slice method returns
selected entries from an array. To return everything BUT the first entry in
arr = ['L', 'C', '1', '0', '1'], use arr.slice(1).
Let's add the bracket notation and the slice method to our function:
1function combineEntries(arrayName){
2 if (arrayName.length <= 1){
3 return arrayName[0];
4 } else {
5 return arrayName[0]+combineEntries(arrayName.slice(1));
6 }
7}
Each time the else statement runs, it extracts the first element in the
array with arrayName[0], then it calls itself with the remaining array
elements (arrayName.slice(1)).
For combineEntries(['L', 'C', '1', '0', '1']);, the sequence would be:
| Step | Description |
|---|---|
| 1 | First call: Combine 'L' with combineEntries(['C', '1', '0', '1']). |
| 2 | Second call: Combine 'C', with combineEntries(['1', '0', '1']). |
| 3 | Third call: Combine '1', with combineEntries(['0', '1']). |
| 4 | Fourth call: Combine '0', with combineEntries(['1']). |
| 5 | Fifth call: Base case returns '1'. |
To get the final result, proceed up the chain:
| Step | Description |
|---|---|
| 5 | Return '1' to the fourth call. |
| 4 | Return '01' to the third call. |
| 3 | Return '101' to the second call. |
| 2 | Return 'C101' to the first call. |
| 1 | Return 'LC101 as the final result. |
Question
What if we wanted to take a number (n) and add it to all of the positive integers below it? For example, if n = 5, the function returns 5 + 4 + 3 + 2 + 1 = 15.
Consider the code sample below, which declares the decreasingSum function.
1function decreasingSum(integer) {
2 if (integer === 1){
3 return integer;
4 } else {
5 //call decreasingSum function again
6 }
7}
Which of the following should be used in the else statement to recursively call decreasingSum
and eventually return the correct answer?
return integer + (integer-1);return integer + (decreasingSum(integer));return integer + (decreasingSum(integer-1));return decreasingSum(integer-1);Experiment with this repl.it.